Skip to main content

687. Longest Univalue Path

문제​

Given the root of a binary tree, return the length of the longest path, where each node in the path has the same value. This path may or may not pass through the root.

The length of the path between two nodes is represented by the number of edges between them.

예제 입출력​

img

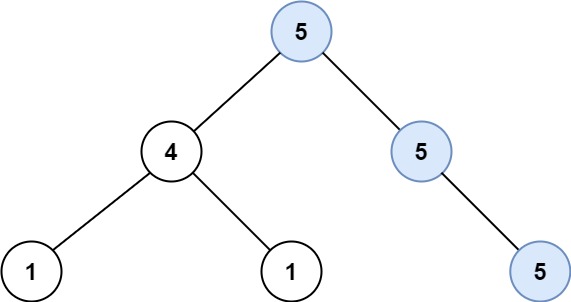
Input: root = [5,4,5,1,1,null,5]
Output: 2
Explanation: The shown image shows that the longest path of the same value (i.e. 5).
참고

You can read the full description here.

풀이 1​

접근법​

  1. DFS로 후위 순회를 하면서 리프노드와의 거리를 매겨줍니다.
  2. 자식 노드와 본 노드의 값이 같을 때만 업데이트합니다.
  3. 양쪽 자식과 모두 값이 다른 경우 리프노드처럼 취급되어 0을 리턴하게 됩니다.

구현 코드​

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    longest: int = 0
    def longestUnivaluePath(self, root: Optional[TreeNode]) -> int:
        def dfs(node: TreeNode) -> int:
            if node == None:
                return -1
            left = dfs(node.left)
            right = dfs(node.right)

            if node.left and node.right and node.val == node.right.val and node.val == node.left.val:
                self.longest = max(self.longest, left + right + 2)
                return max(left, right) + 1
            elif node.left and node.val == node.left.val:
                self.longest = max(self.longest, left + 1)
                return left + 1
            elif node.right and node.val == node.right.val:
                self.longest = max(self.longest, right + 1)
                return right + 1
            else:
                return 0

        dfs(root)
        return self.longest

복잡도 분석​

  • nn: 노드의 수
  • 시간복잡도: O(n)O(n)

책에 있는 풀이​

참고

원본 코드는 여기에서 확인하실 수 있습니다.

풀이 2​

접근법​

  1. 풀이 1과 유사합니다.

image

구현 코드​

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None


class Solution:
    result: int = 0

    def longestUnivaluePath(self, root: TreeNode) -> int:
        def dfs(node: TreeNode):
            if node is None:
                return 0

            # 존재하지 않는 노드까지 DFS 재귀 탐색
            left = dfs(node.left)
            right = dfs(node.right)

            # 현재 노드가 자식 노드와 동일한 경우 거리 1 증가
            if node.left and node.left.val == node.val:
                left += 1
            else:
                left = 0
            if node.right and node.right.val == node.val:
                right += 1
            else:
                right = 0

            # 왼쪽, 오른쪽 자식 노드간 거리의 합 최대값이 결과
            self.result = max(self.result, left + right)
            # 자식 노드 상태값 중 큰 값 리턴
            return max(left, right)

        dfs(root)
        return self.result

복잡도 분석​

  • nn: 노드의 수
  • 시간복잡도: O(n)O(n)